LES MATRICES A QUOI CA SERT?

Par Axone Man ( contact : axoneman01@infonie.fr )

L'idée des matrices est venue après avoir lu et relu la « Théorie des formes » de Didier BONIN. Cette théorie explique en détail les effets de la répartition des masses et des portances sur l'ensemble du cercle balayé, Ultimatrix permet de mesurer cette répartition.

Avant toute chose, il faut trouver le CG (Centre de gravité) du boomerang en tenant compte de son lest éventuel. Chaque modification de forme mais aussi de plombage modifie l'emplacement du CG et donc les qualités d'un boomerang.

Les abréviations utilisées dans ce papier sont:

CG: centre de gravité

CB: cercle balayé

0PT: zone 0 portance 0 traînée

ML: matrice linéaire

Voici comment on peut définir les différentes zones d'un boomerang d'après son CG:

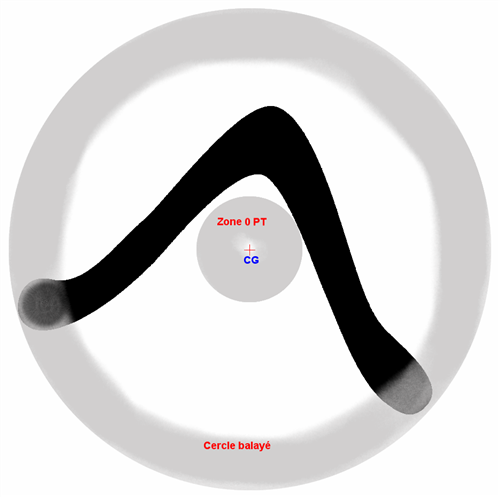
A partir du CG, le cercle balayé est bien visible, dans ce cas c'est la pale de suite qui borde le CB. Dans certains cas, comme celui-ci, il existe au sein du CB une zone vide où aucune matière n'est présente lors de la rotation, c'est la zone 0PT, pas de traînée, pas de portance. On peut aussi l'appeler cercle d'évidement mais il faut garder à l'esprit que cette zone est tout sauf neutre. La réduire ou l'augmenter modifie les performances du boomerang.

La preuve ci-dessous:

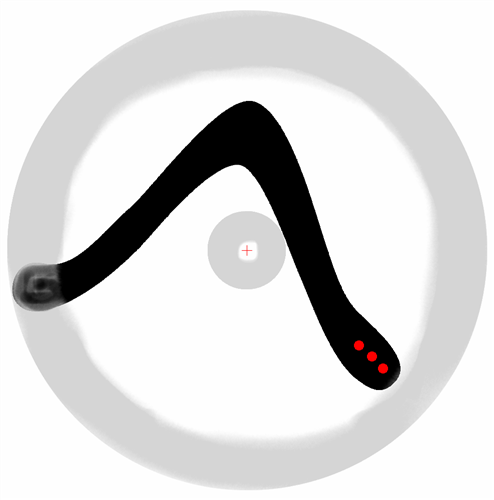
Vous constatez sans peine le décalage du CB ainsi que la modification de la zone 0PT, bien rétrécie. Tout cela a évidemment des répercussions sur la trajectoire du boomerang. Pour trouver le CG avec Ultimatrix vous pouvez calculer une matrice ou demander le calcul du CG à part.

Vous disposez pour celà du menu. Calcul -> CG, raccouri clavier ATL C + C

Pour calculer une matrice: Calcul -> Matrice, raccourci clavier: ALT C + M

Prenons par exemple ce boomerang classique, avec et sans lest :

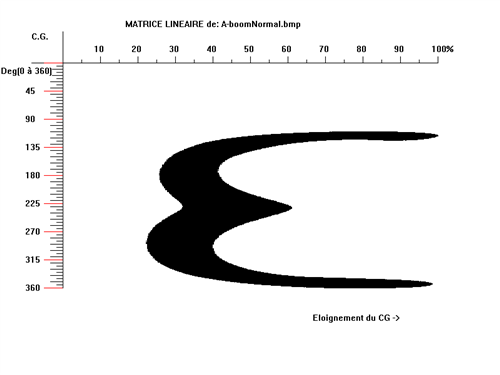
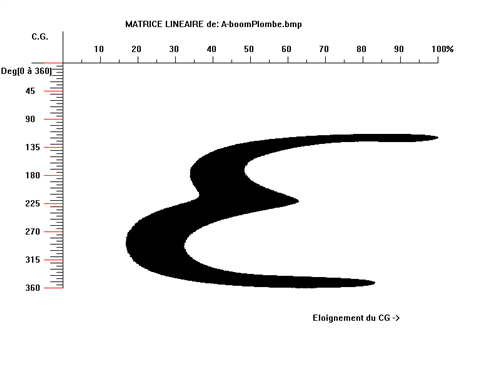
Et si les regarder ne suffit pas, voilà les deux matrices superposées:

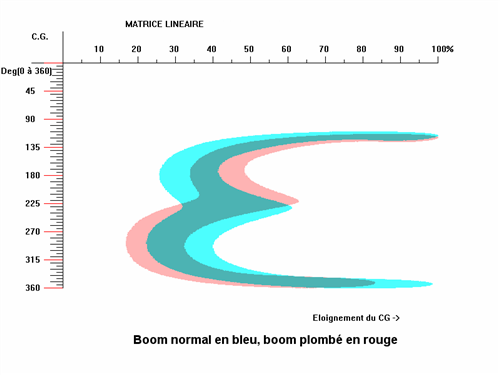
Là c'est clair, le déplacement du CG a des répercutions.

Passons maintenant à ce que l'on peut voir avec les matrices: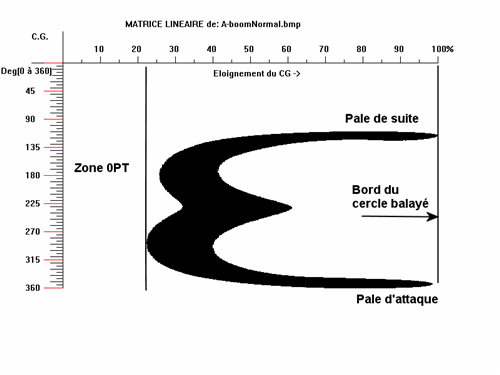

En abscisse on trouve le CG à gauche et le bord du CB à droite, en ordonnée on trouve le CG en haut et les lignes de récupération degré par degré, de 1 à 360.

Avec ces renseignements il est facile de trouver la zone 0PT et de retrouver les pales du boomerang. La zone vide en haut du graphique est donc le « vide » situé entre les pales.

On y voit plus clair avec ce dessin: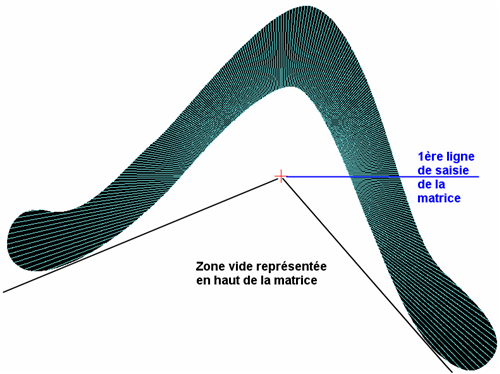

La matrice est saisie depuis la ligne bleue (1ere ligne de saisie de la matrice) en tournant dans le sens horaire, degré par degré. Une matrice est donc composée de 360 lignes d'une longueur égale à la taille du CB, c'est l'empilement vertical des 360 lignes.

Par convention, elle est remise en forme pour assurer qu'elle ne soit pas modifiée par la position du boomerang à analyser. Cette mise en forme se fait selon deux cas. Dans le premier cas la matrice est « trouée », c'est le cas avec ce boomerang. Par « trouée » il faut entendre qu'il existe des lignes vides (pas de rencontre de matière) dans la matrice. Dans ce cas précis, les lignes vides sont représentées en premier, d'où le vide en haut du graphique.

Pour les boomerangs dont la matrice est pleine (en opposition avec les trouées), c'est la ligne qui traverse le moins de matière qui est affichée en premier. Cette façon de représenter les matrices leur assure une homogénéité quelle que soit la position du boomerang sur l'image à analyser.

Passons maintenant aux sommes de ces matrices, elles apportent aussi des renseignements.

Pour calculer la somme horizontale:

Matrice linéaire -> Somme horizontale, raccourci clavier: ALT M + H

Somme horizontale:

D'abord voyons ce qu'est cette somme. C'est une matrice dont on n'indique plus l'éloignement au CG mais dont on récupère simplement la matière rencontrée ligne après ligne. Pour synthétiser on pourrait dire que c'est les lignes de la matrice qui sont affichées sans tenir compte des endroits où il n'y a pas de matière. La zone 0PT est donc invisible mais la zone vide du haut de la matrice demeure. La récupération des quantités de matière est effectuée ligne par ligne, degré par degré donc.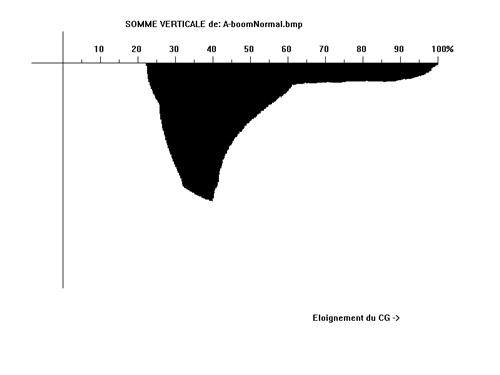

Matrice linéaire -> Somme verticale, raccourci clavier: ALT M + V

Somme verticale:

Cette fois l'échelle qui ne change pas est celle qui lie le CG et le bord du CB, l'abscisse. C'est juste une somme de la matière contenue dans les colonnes plutôt que dans les lignes comme pour la somme horizontale. Comme la somme horizontale la matière est récupérée colonne par colonne et représentée de haut en bas.

Somme horizontale compensée:

Matrice linéaire -> Somme horizontale compensée. Raccourci clavier: ALT M + O

Cette fois on aborde la compensation. Quesako? Simple, on prend en compte l'éloignement de la matière par rapport au CG. Chaque « point » de matière rencontré est le carré de sa distance au CG.

Cela assure une représentation de la portance qui elle aussi augmente au carré de la vitesse. Pour assurer que le graphique ne débordera pas de la fenêtre, il est systématiquement normalisé sur l'axe des abscisses.

Pour la somme horizontale compensée donc, on a une représentation de la portance degré par degré.

Vous remarquerez que comme toute somme horizontale, on y retrouve la zone vide correspondant à l'écart entre les pales.

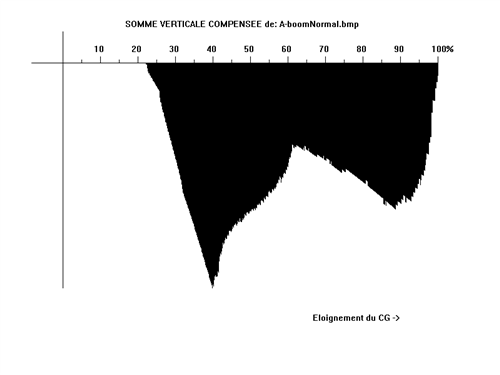
Matrice linéaire -> Somme verticale compensée, raccourci clavier ALT M + E

Somme verticale compensée:

Le même principe de compensation est appliqué, la normalisation est faite cette fois sur l'axe des ordonnées. C'est une représentation de la portance non plus angulaire mais selon l'éloignement au CG. Comme toute somme verticale on y retrouve la zone 0PT.

Appliqué à ce boom voici ce qu'on peut observer:

Sommes horizontales:

On y retrouve la structure du boomerang, les pales et le coude, comme sur la matrice. Sur la somme horizontale compensée il est clair que ce sont les deux pales qui génèrent l'essentiel de la portance, et que la répartition de la portance est bien répartie entre les deux pales avec une très légère prédominance de la pale de suite. La somme horizontale ordinaire montre juste qu'il y a plus de matière sur une pale que sur le coude, on l'aurait deviné ;-)

Sommes verticales:

Là d'autres renseignements nous attendent, cette fois c'est la répartition de la matière depuis le CG jusqu'au bord du CB qui est affichée. Ainsi sur la somme verticale normale on voit sans peine qu'il y a presque 25% de la distance CG- bord extérieur du CB qui ne comporte aucune matière (la zone 0PT). Ensuite elle se répartit plutôt autour de 40% de la distance CG- bord extérieur du CB où on trouve le pic. Une fois compensée cette somme nous indique que le maximum de portance est situé toujours à 40% mais on y voit très bien que plus on s'éloigne du CG et plus la matière porte. Ainsi un petit peu de matière sur la somme normale devient important sur la compensée, par exemple ici à 85% de la distance CG- bord extérieur du CB. Autrement dit la matière des pales porte à elle toute seule presque autant que la matière plus vaste du coude.

Remarquez au passage que l'ancienne zone appelée neutre qui englobait le coude est tout sauf neutre, il n'existe rien de neutre sur un boomerang.

petit mode d'emploi

Limitations et obligations: Ultimatrix est un programme prototype et est loin de sa version définitive, il souffre donc de limitations que vous devez connaître pour en tirer le maximum. En premier lieu les images qu'il accepte sont des .bmp 24 bits au format 800 x 600 pixels exclusivement. Pour représenter un boomerang vous devez le dessiner en noir (RGB &000000 ou 0,0,0) sur fond blanc (RGB &FFFFFF ou 255,255,255). Les lests éventuels sont représentés par la couleur rouge (RGB &FF0000), Vert (RGB &00FF00) et Bleu (RGB &0000FF). Ces valeurs doivent être scrupuleusement respectées.

Considérant maintenant que les images qui lui seront présentées seront conformes à ce qu'il peut traiter, voilà ce que peut en déduire Ultimatrix.

Calculer -> CG: C.G. Centre de gravité: Chargez une image et le programme vous indiquera le CG du boomerang. Les positions x et y sont données et une icône se place au centre de gravité. Vous pouvez choisir un mode de calcul pour un boomerang sans plombage (mode monochrome), un mode de calcul à deux couleurs (+ le blanc du fond évidemment) pour un boom noir et un plombage rouge, et un mode « toutes couleurs » pour des booms jusque 4 densités. Par défaut le mode de calcul du CG est réglé sur « rouge » (deux couleurs) et la densités pour le noir est de 0,75 (contre plaqué) et celle du noir est à 11,3 (densité du plomb). Les modes de calcul et les valeurs attribuées aux couleurs doivent être modifiées avant de saisir l'image. Evidemment le CG est trouvé beaucoup plus rapidement avec une seule couleur qu'avec quatre, Ultimatrix n'étant pas pas vraiment un monstre de rapidité je vous invite à ne calculer qu'avec les couleurs qui vous sont nécessaires.

Calculer -> Matrice Linéaire: Matrice linéaire: Chargez une image et le programme récupérera la matrice linéaire après avoir récupéré le CG nécessaire au calcul. A partir de ce moment vous pouvez voir la matrice, sauvegarder le fichier matrice par le menu « Sauvegarde » et voir les sommes qui en découlent par le menu « Matrice linéaire »

Matrice linéaire -> Charger un fichier matrice: Pour pouvoir voir une matrice sans avoir à la recalculer.

Matrice linéaire -> Afficher matrice en cours

Matrice linéaire -> Somme horizontale

Matrice linéaire: -> Somme verticale

Matrice linéaire: -> Somme horizontale compensée

Matrice linéaire: -> Somme verticale compensée

A propos: Juste un petit coucou ;-)

Licence: Ce programme est GRATUIT et peut être distribué librement pourvu que ce soit gratuitement. Vous pouvez faire ce que vous voulez de ce programme à la seule condition de ne pas le vendre. Ce programme est distribué sans aucune garantie d'aucune sorte, vous l'utilisez à vos risques et périls sous votre entière responsabilité. L'usage ou la possession de ce programme implique acceptation pleine et entière de cette licence.

Copyright Ultimatrix Team 2005

Ultimatrix Team: Axone Man, Renan Guillou, Laurent Blanchard

Je vous souhaite de bonnes recherches... et trouvailles.

Have du FUN!!!

Axone Man
( contact : axoneman01@infonie.fr )

Quelques renseignements possiblement pratiques:

Pour des captures d'écran faciles et efficaces, Xnview est un visualisateur/convertisseur très complet et entièrement gratuit, disponible ici: www.wnview.com